形状距離の特長
形状距離は、「周波数のずれ」や「時間のずれ」の大きさを検出します
音声のパワースペクトルでは、ホルマントと呼ばれる複数のピークが観測されます。
ホルマントピークでは、同じ音声であっても、発声ごとにピーク周波数が変動する「周波数のずれ」やピーク時間が変動する「時間のずれ」が現れます。
図1Aは、標準音声としてパワースペクトルに2個のピークをもち、入力音声1、2、3としてピーク位置がそれぞれ異なる例を示しています。なお、標準音声のエネルギーと各入力音声のエネルギーは等しくなっています。
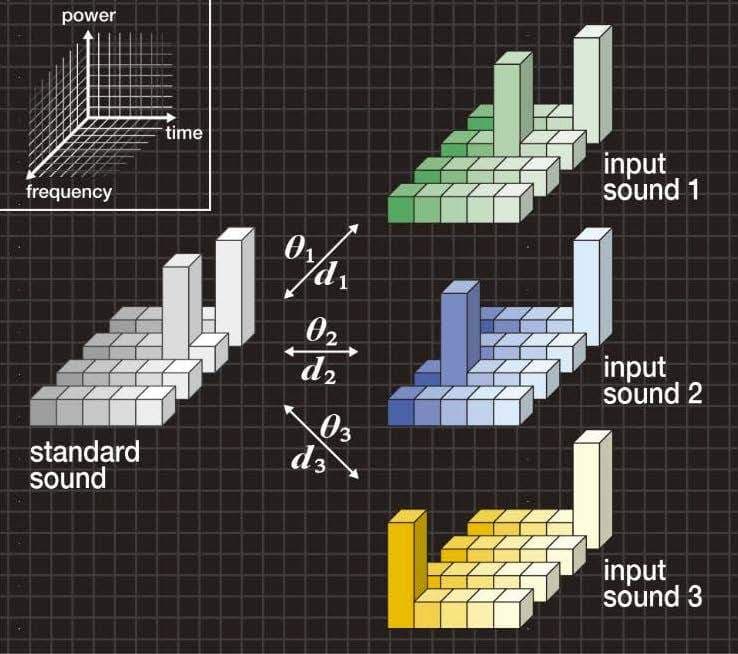
図1A 「ピークのずれ」の典型例
図1Bの左の棒グラフは、標準音声と各入力音声1、2、3との間のコサイン尺度θ1、θ2、θ3を示していますが、従来のコサイン尺度ではθ1=θ2=θ3となるため、3つの入力音声を区別できません。
図1Bの右の棒グラフは、標準音声と各入力音声1、2、3との間の形状距離d1、d2、d3を示しています。形状距離では、「周波数のずれ」や「時間のずれ」の大きさを検出して、3つの入力音声を区別できます。
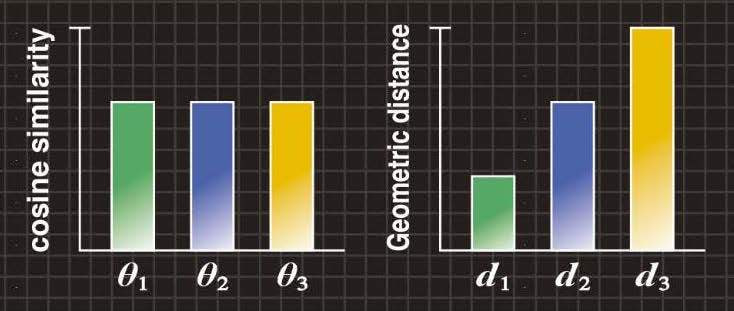
図1B コサイン尺度と形状距離
従来のコサイン尺度の計算式
標準画像(標準音)の特徴量を成分si(i=1, 2,..., n)とする標準パターンベクトルsと、入力画像(入力音)の特徴量を成分xi(i=1,2,..., n)とする入力パターンベクトルxを作成して、次式のように表現します。
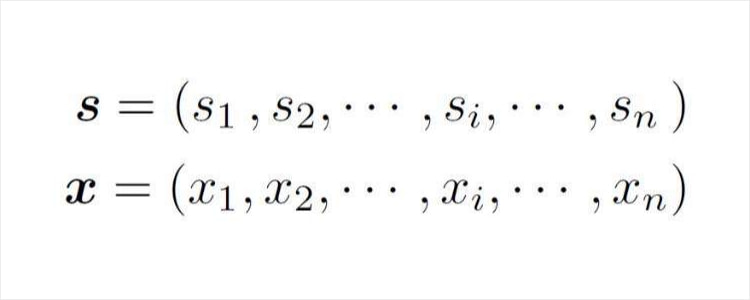
このとき、従来のコサイン尺度は次式により算出されます。なお、図1B~4Bは、アークコサインを用いて算出される角度θを示しています。
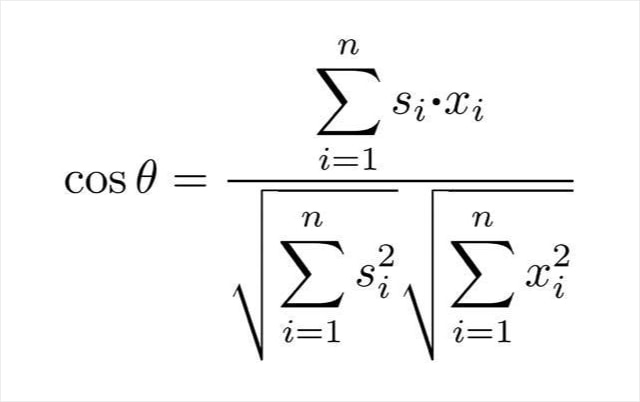
形状距離は、「スペクトル強度のゆらぎ」を吸収します
摩擦音 /s/ では、平坦なパワースペクトルが観測されます。摩擦音のパワースペクトルでは、平坦であっても、発声ごとに形状が変動する「スペクトル強度のゆらぎ」が現れます。
図2Aは、標準音声として平坦なパワースペクトルをもち、入力音声4、5として標準音声に「スペクトル強度のゆらぎ」が発生し、入力音声6として1個のピークをもつ例を示しています。ここで、各パワースペクトルには、変数αについて図中に示す関係があるため、標準音声のエネルギーと各入力音声のエネルギーは等しくなります。
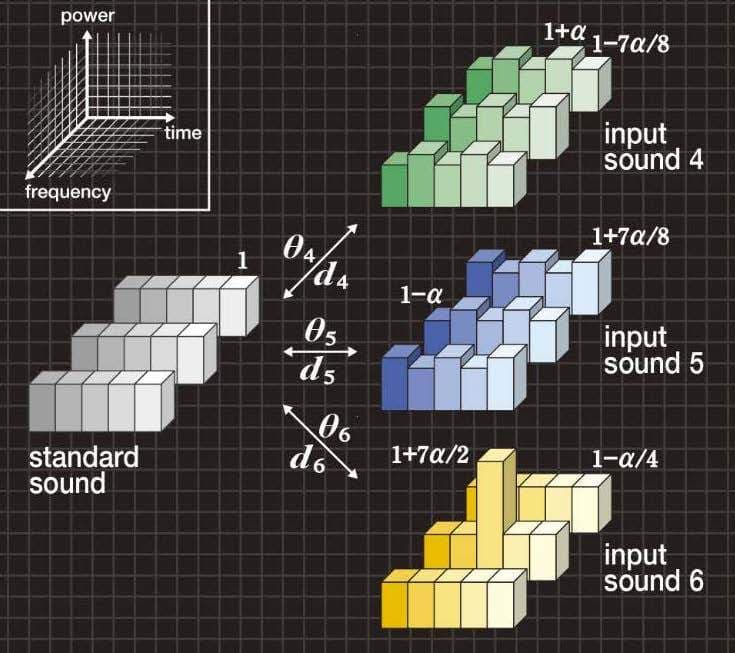
図2A 「ゆらぎ」の典型例
図2Bの左の棒グラフは、標準音声と各入力音声4、5、6との間のコサイン尺度θ4、θ5、θ6を示していますが、従来のコサイン尺度ではθ4=θ5=θ6となるため、3つの入力音声を区別できません。
図2Bの右の棒グラフは、標準音声と各入力音声4、5、6との間の形状距離d4、d5、d6を示しています。形状距離では、「スペクトル強度のゆらぎ」を吸収して、入力音声4、5と入力音声6を区別できます。
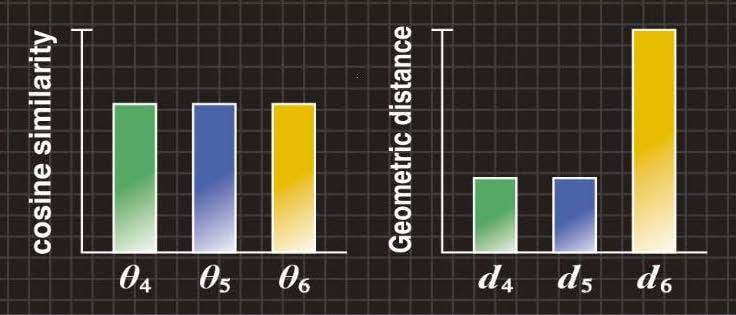
図2B コサイン尺度と形状距離
形状距離は、「位置ずれ」の大きさを検出します
手書き文字では、同じ文字であっても、筆記ごとに線の位置が変動する「位置ずれ」が現れます。
図3Aは、記号“+”の標準画像と、横線の位置がそれぞれ異なる入力画像1、2、3を示しています。
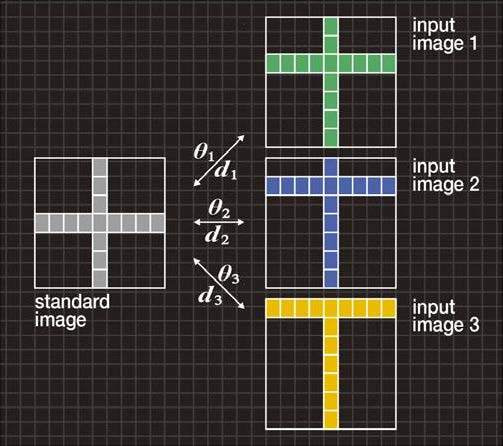
図3A 「位置ずれ」の典型例
図3Bの左の棒グラフは、標準画像と各入力画像1、2、3との間のコサイン尺度θ1、θ2、θ3を示していますが、従来のコサイン尺度ではθ1=θ2=θ3となるため、3つの入力画像を区別できません。
図3Bの右の棒グラフは、標準画像と各入力画像1、2、3との間の形状距離d1、d2、d3を示しています。形状距離では、「位置ずれ」の大きさを検出して、3つの入力画像を区別できます。
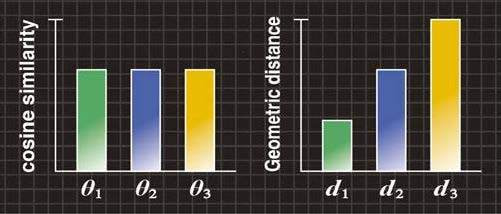
図3B コサイン尺度と形状距離
形状距離は、「文字の変形」を吸収します
手書き文字では、同じ文字であっても、筆記ごとに線の位置や長さが変動する「文字の変形」が現れます。
図4Aは、アルファベット“E”の標準画像と、それぞれ“E”、“F”、“G”の入力画像4、5、6を示しています。
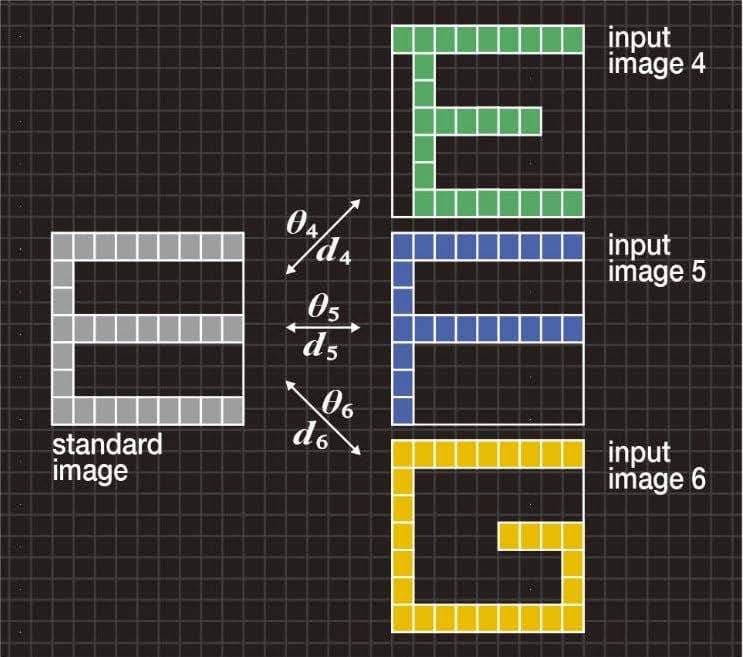
図4A 「文字の変形」の典型例
図4Bの左の棒グラフは、標準画像と各入力画像4、5、6との間のコサイン尺度θ4、θ5、θ6を示していますが、従来のコサイン尺度ではθ4>θ5>θ6となるため、アルファベット“E”を正しく認識できません。
図4Bの右の棒グラフは、標準画像と各入力画像4、5、6との間の形状距離d4、d5、d6を示しています。形状距離では、「文字の変形」を吸収して、アルファベット“E”を認識できます。
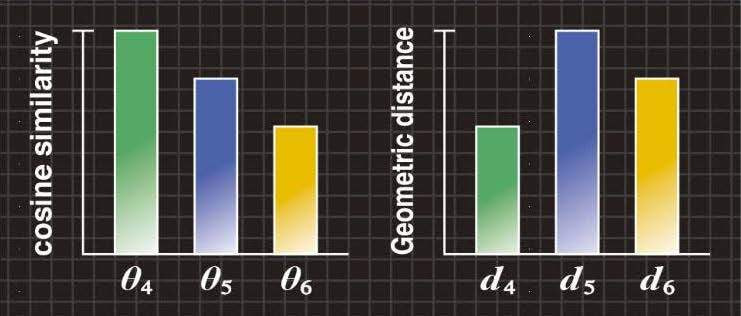
図4B コサイン尺度と形状距離
1次元パターン間の形状距離を求めます
図5は、機械音の瞬間のパワースペクトルを示しています。このような標準音と入力音の間の形状距離dが求められます。
形状距離は、機械運転による「スペクトル強度のゆらぎ」の中で、スペクトルピークの「強度変化」や「周波数のずれ」を検出します。
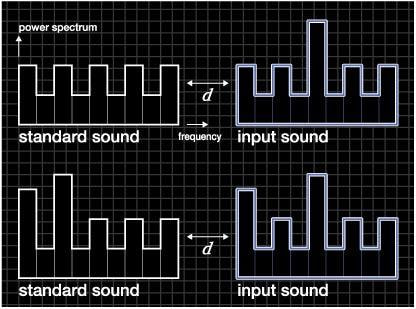
図5 瞬間パワースペクトルの典型例
新しい類似性尺度GDは、雑音などの「ゆらぎ」の中で 標準パターンと入力パターンにピークの「ずれ」が生じたとき、 「ゆらぎ」を吸収しながら「ずれ」の増加とともに単調増加します。
従来のユークリッド距離やコサイン尺度では、標準パターンと入力パターンの対応する成分ごとに演算(one-to-one mapping)を行っていますが、周囲の成分との相互関係を考慮していません。このため、雑音などの「ゆらぎ」に弱く、また、標準パターンと入力パターンに局所的な「ずれ」が生じたときには演算値が階段状に変化してしまいます。
形状距離では、パターン間の距離値が人間の感覚を実現するように、周囲の成分との相互関係を考慮した演算(one-to-many point mapping)を行います。これにより、雑音などの「ゆらぎ」の中で、標準パターンと入力パターンに局所的な「ずれ」が生じたとき、「ずれ」の増加とともに単調増加する距離値が得られます。
形状距離の原理
数学モデルの仮定
類似性尺度は、聴覚や視覚など人間の感覚に関わる概念です。このため、コンピュータを用いて数値処理を行う場合、類似性尺度について最初に数学モデルを仮定することが必要になります。ここでは、ユークリッド距離やコサイン尺度などがもつ上記の問題を改善するように、次の2つの条件をもつ数学モデルを仮定します。
雑音などの「ゆらぎ」に対して距離値の変動が小さいこと
標準パターンと入力パターンのピークの「ずれ」の増加とともに距離値が単調増加すること
図1B、図2Bおよび図3Bそれぞれの右側の棒グラフは、数学モデルを表現しています。
アルゴリズムの開発
次に、上記の数学モデルを実現する新しいアルゴリズム(GDアルゴリズム)を提案します。統計解析の分野において、正規分布は多くの現象のモデルとして使われています。そこで、注目する現象が正規分布に従うことを確かめる必要があり、そのために「尖度(Kurtosis)」と「歪度(Skewness)」という統計量が用いられます。図6に示すように、形状距離では、標準パターン(standard pattern)と入力パターン(input pattern)の間の形状差δを、正規分布の値をもつ基準パターン(reference pattern)の形状変化δに置き換えます。そして、基準パターンの形状変化の大きさを「尖度」と「歪度」の変化量として数値化し、距離値として出力します。これにより、パターンの各成分と周囲の成分との相互関係を反映した類似性尺度が得られます。
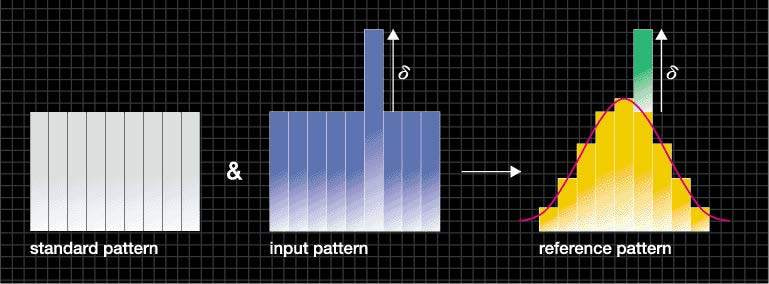
図6 標準パターン、入力パターン、基準パターンの関係
なお、図7に示すように、尖度の値aは、現象の分布形状が正規分布に従っているときはa=3になり、正規分布より尖った分布のときはa>3になり、反対に、正規分布よりなだらかな分布のときはa<3になることが知られています。
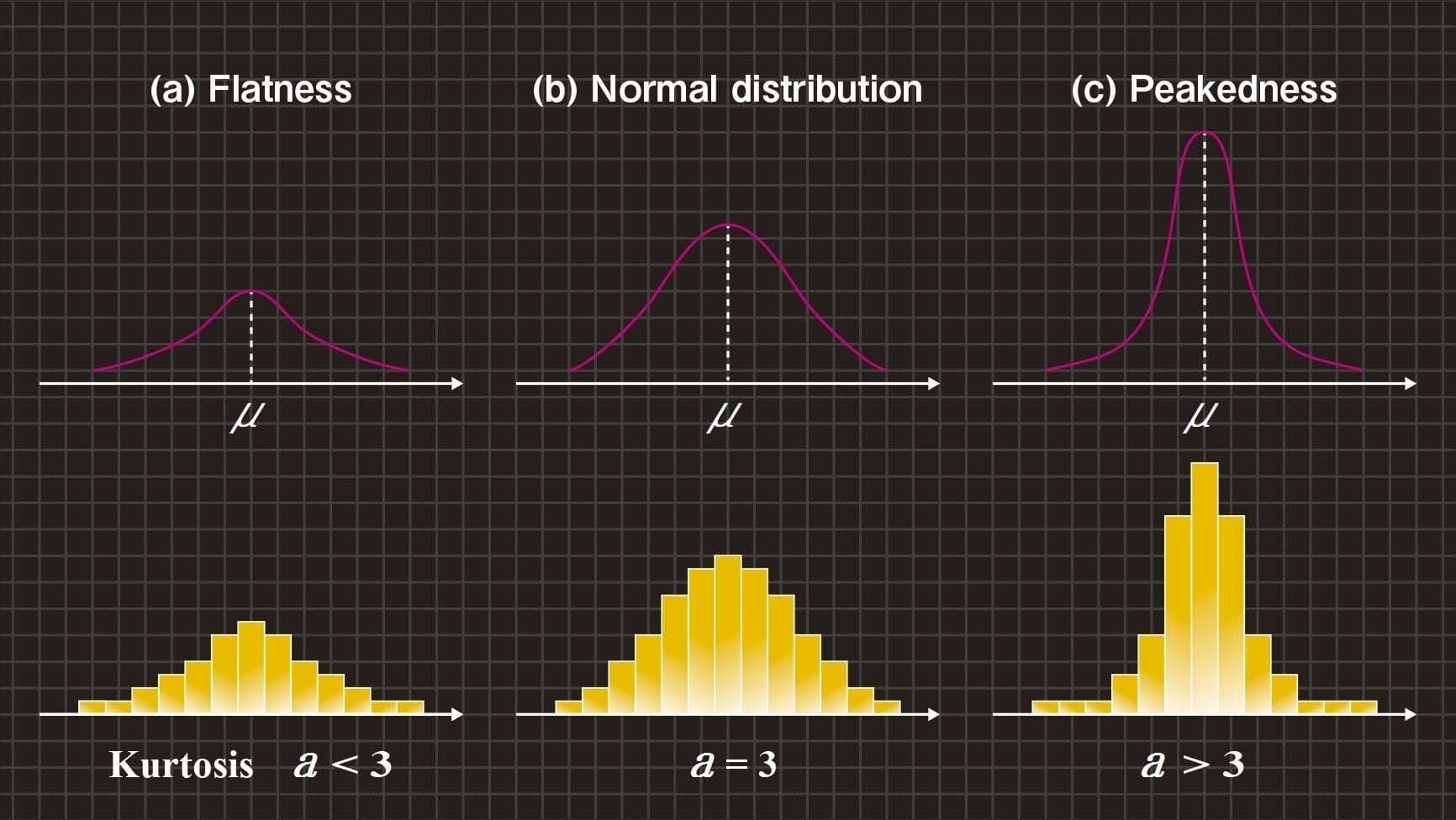
図7 尖度の特徴
また、図8に示すように、歪度の値bは、現象の分布形状が中心に関して左右対称であるときはb=0になり、右に裾が長い分布のときはb>0になり、反対に、左に裾が長い分布のときはb<0になることが知られています。
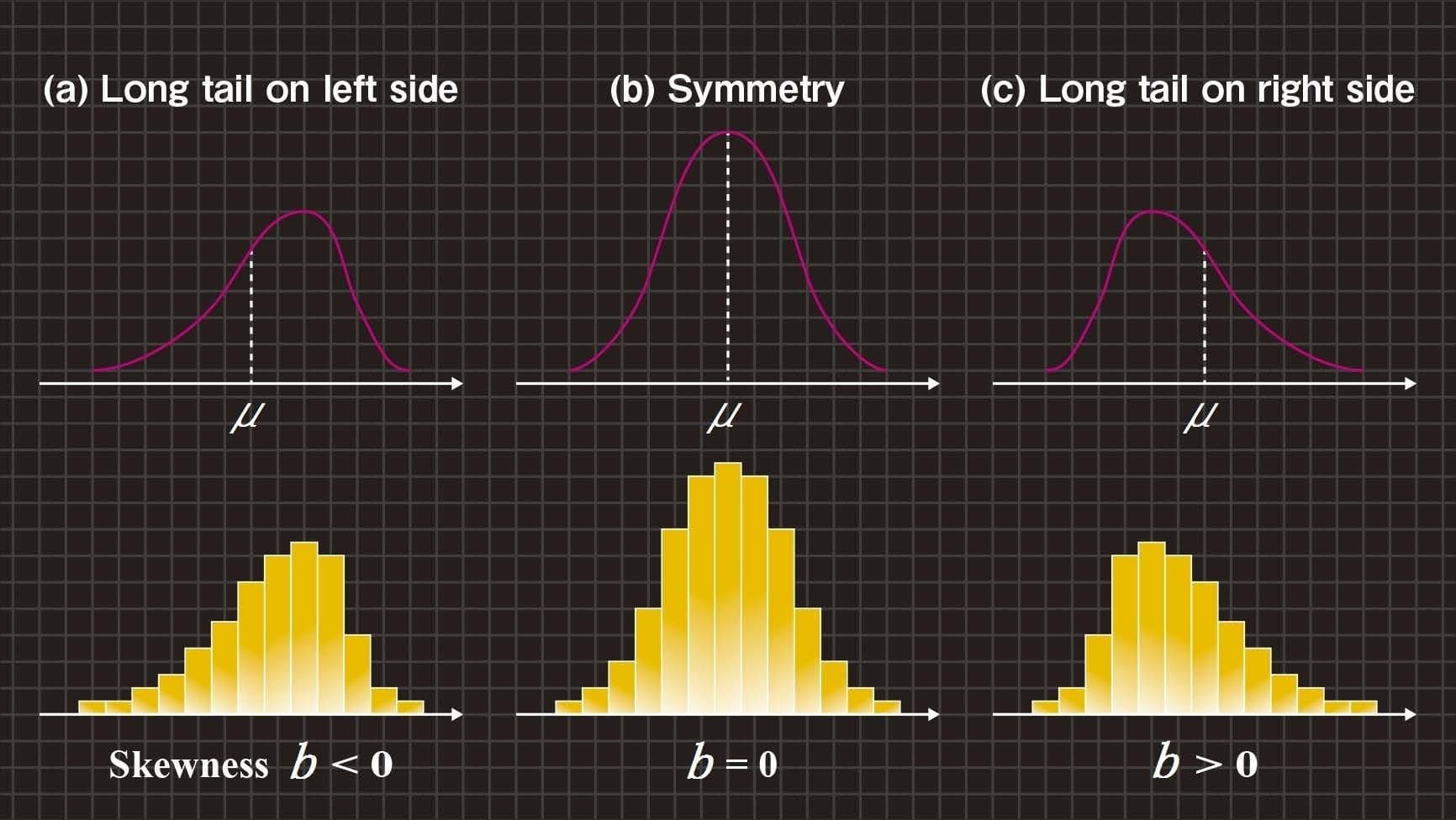
図8 歪度の特徴
ここで、図9と図10を用いてGDアルゴリズムを説明します。
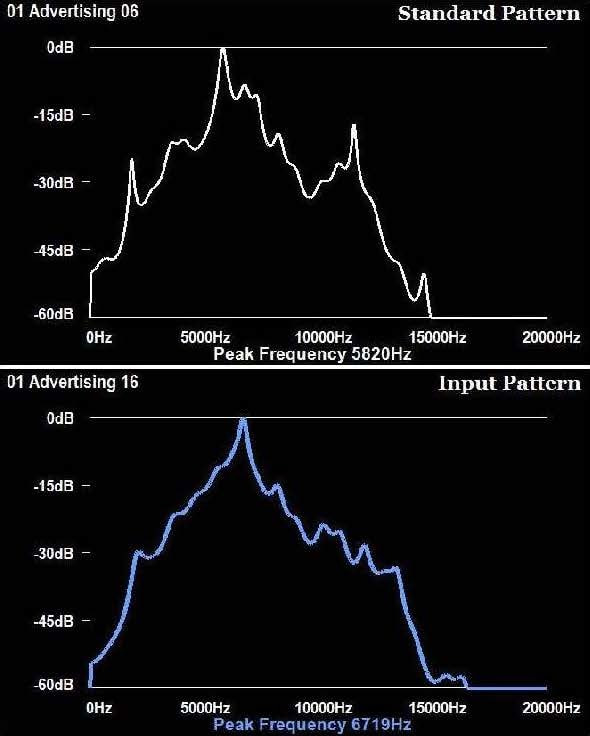
図9 標準パターンと入力パターン
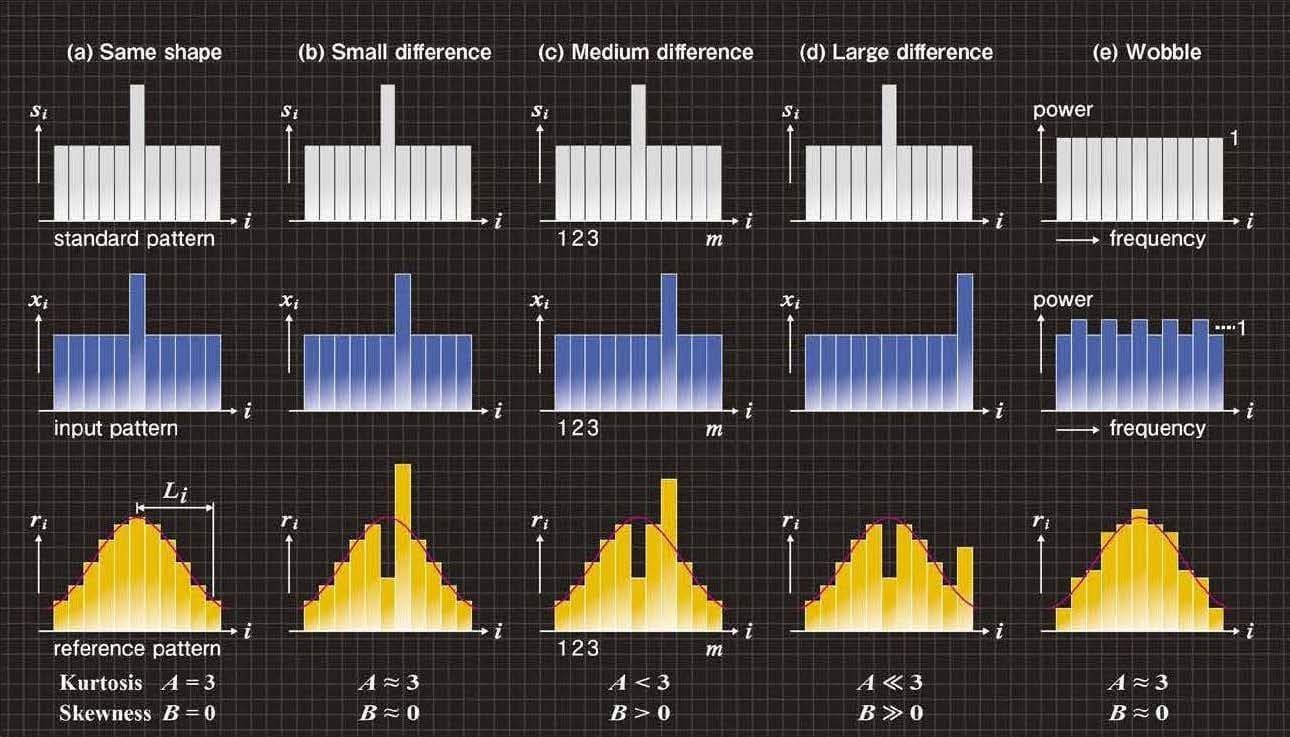
図10 基準パターンの形状変化
図9は、Macleay's Fig Parrot(Cyclopsitta diophthalma macleayana)と呼ばれる鳥の鳴き声から抽出した音響スペクトル(周波数-パワー)を示しています。同時に、図9は、標準音と入力音の瞬間パワースペクトル(周波数-パワー)を用いて作成した標準パターンと入力パターンを示したものです。また、図10(a)-(e)は図9の模式図であり、それぞれ標準パターンと入力パターンの典型例を示しています。ただし、パワースペクトルはm個の周波数帯域をもつフィルタバンクの出力から生成したものとします。
また、標準音と入力音のi番目(i=1,2,・・・m)のパワースペクトルの値をそれぞれの総エネルギーで除算し、正規化パワースペクトルsi及びxiを算出したものとします。このとき、標準パターンと入力パターンの面積は等しくなります。
そして、siを成分とする標準パターンベクトルsと、xiを成分とする入力パターンベクトルxを作成して、式(1)のように表します。式(1)は、標準パターンと入力パターンの形状をそれぞれベクトルのm個の成分値で表現したものです。
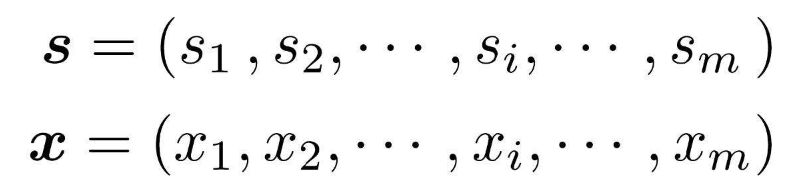
式(1)
さらに、図10(a)-(e)は、それぞれ初期値が正規分布の関数値riと同じ高さをもつ棒グラフを示しています。そして、riを成分とする基準パターンべクトルrを作成して、式(2)のように表します。式(2)は、正規分布の形状をベクトルのm個の成分値で表現したものです。
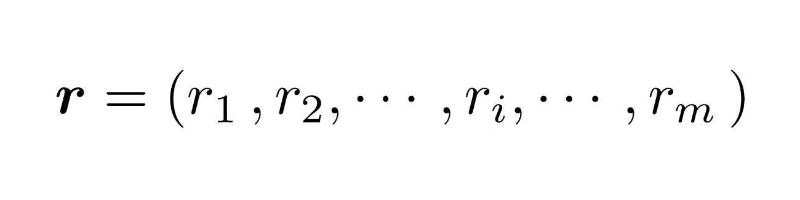
式(2)
GDアルゴリズムでは、式(3)を用いて標準パターンと入力パターンの間の形状差を基準パターンの形状変化に置き換えます。

式(3)
次に、図10(a)-(e)を用いて式(3)を説明します。
図10(a)は、標準パターンと入力パターンが同じ形状をもつ場合の例です。このとき、式(3)のriの値は変化しませんので、図10(a)に示す基準パターンは正規分布から形状の変化はありません。
図10(b)-(d)は、標準パターンと入力パターンの間でピークのずれが小さい場合、中程度の場合、大きい場合の例をそれぞれが示しています。もし、式(3)を形状で表現するならば、図10(b)-(d)に示すように、それぞれの標準パターンのピーク位置iにおいてriの値が減少すると同時に、それぞれの入力パターンのピーク位置iにおいてriの値が増加します。
図10(e)は、平坦な形状をもつ標準パターンと、平坦な形状の上に「ゆらぎ」が発生した入力パターンの典型例を示しています。このとき、式(3)においてriの値は交互に増加減少するため、図10(e)に示す基準パターンでは正規分布から形状の変化が小さくなります。
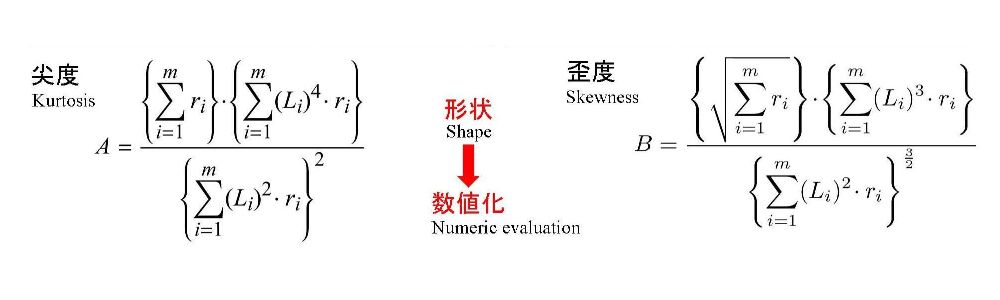
式(4)
GDアルゴリズムでは、図7と図8に示す平均値μを、図10(a)に示す正規分布(基準パターン)の中心軸で置き換えます。したがって、”尖度a”と”歪度b”は、式(4)に示す”尖度A”と”歪度B”により置き換えられます。なお、図10(a)の基準パターンに示すように、Li(i=1,2,・・・m)は正規分布の中心軸からの偏差を表しています。
式(3)により形状変化した基準パターンについて、その形状変化の大きさを、”尖度A”と”歪度B”により数値化します。基準パターンの尖度と歪度は、式(4)を用いて算出できます。図10(a)-(e)は、riの値の変化により、AとBの値がどのように変化するかを示しています。
図10(a)では、riの値に変化はなく、尖度はA=3、歪度はB=0になります。
図10(b)では、減少したriの位置iと増加したriの位置iが接近しています。増加と減少の効果が打ち消されて、尖度はA≈3、歪度はB≈0になります。
図10(d)では、基準パターンの形状が正規分布よりもなだらかであり、かつ、正規分布の形状が右に裾が長いので、尖度はA<<3、歪度はB>>0になります。
図10(c)では、基準パターンの形状は(b)と(d)の中間であるため、尖度はA<3、歪度はB>0になります。
図10(e)では、基準パターンの形状は正規分布から変化が小さいため、尖度はA≈3、歪度はB≈0になります。
図10(a)-(d)より、|A|と|B|の値はそれぞれ、標準パターンと入力パターンのピークの「ずれ」の増加とともに単調増加することが分かります。また図10(e)より、「ゆらぎ」についてはA≈3、B≈0になることが分かります。
このように、新しい類似性尺度GD は、雑音などの「ゆらぎ」の中で標準パターンと入力パターンにピークの「ずれ」が生じたとき、「ゆらぎ」を吸収しながら「ずれ」の増加とともに単調増加します。
以上の説明より、GDアルゴリズムが数学モデルとを満たすことが確認できます。
評価実験
参考論文 No.10
上記のGDアルゴリズムの有効性を確認するために、Macleay’s Fig-Parrotと呼ばれる鳥の鳴き声について認識実験を行いました。
図11は、騒音環境下であっても、GDアルゴリズムを用いたパターンマッチングが正確に行われることを示しています。
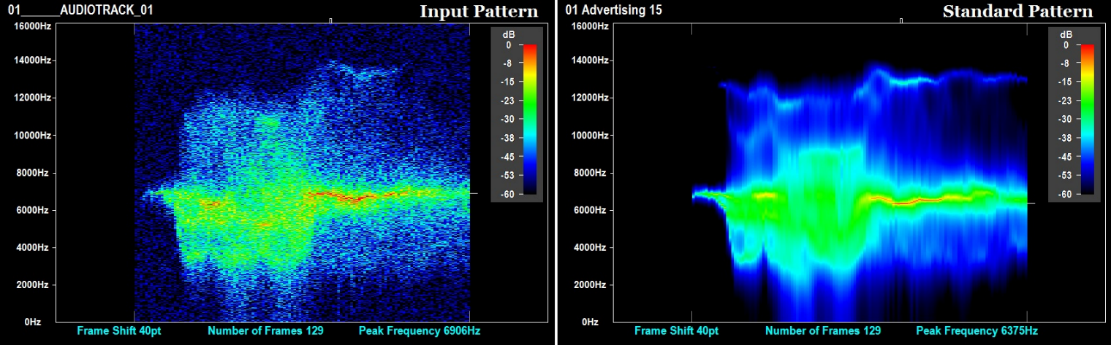
図11 騒音環境下における鳥の鳴き声認識のパターンマッチングの結果
参考論文 No.12
正常なコンクリート、及び、腐食による空洞をもつ異常なコンクリートの表面をたたいた時に発生する音を比較してコンクリート内部の空洞を見つけることにGDアルゴリズムが利用されています。
図12は、ハンマーを用いてコンクリート供試体をたたいた時に発生する音の測定方法を示しています。
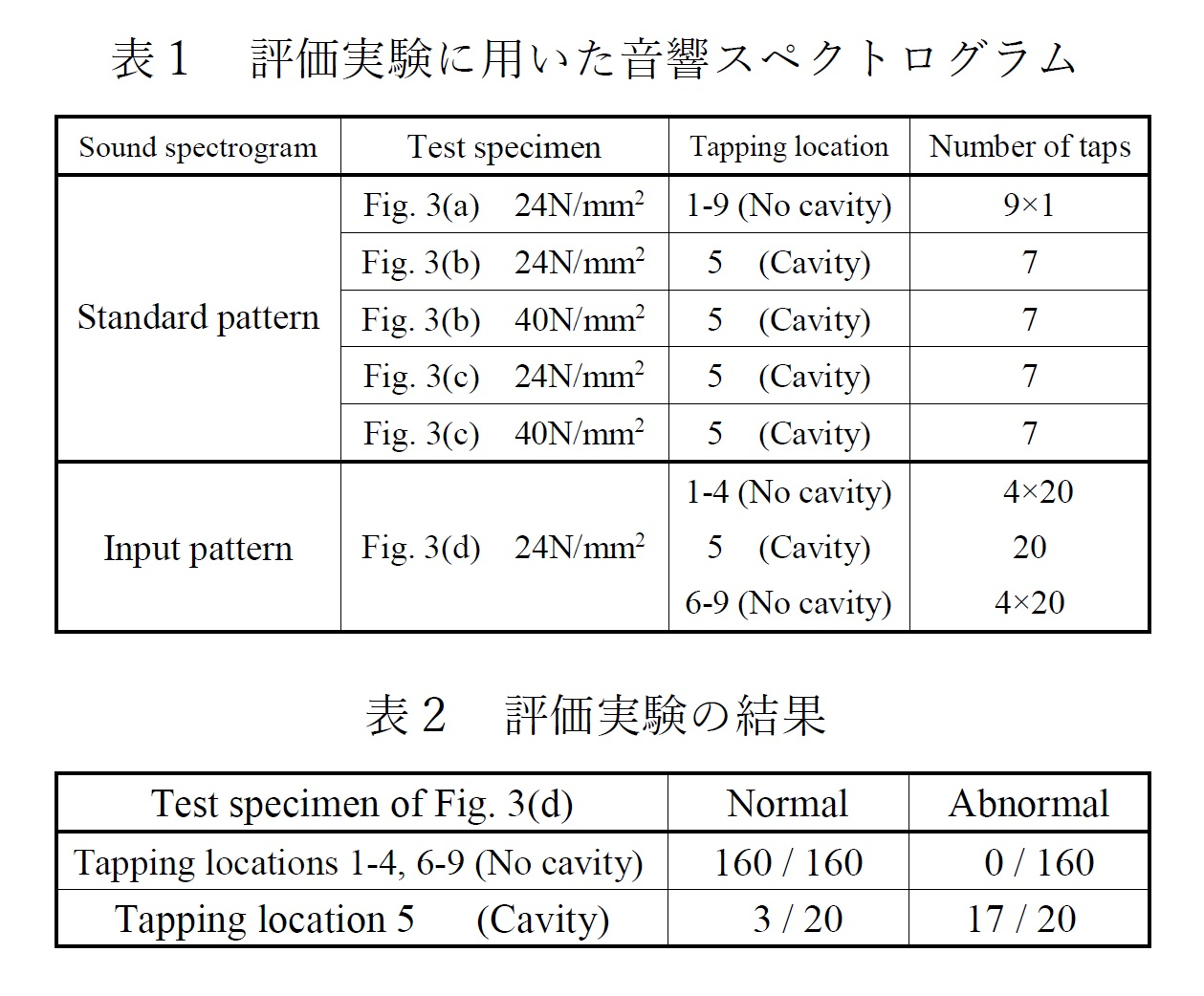
表1は、標準パターンと入力パターンに用いた供試体の種類を示しています。
表2に、評価実験の結果を示します。表2より、空洞から離れた位置1~4及び6~9をたたいた音(入力パターン)はすべて「正常」と認識され、空洞の上の位置5をたたいた音(入力パターン)は17/20が「異常」と認識されたことが分かります。この評価実験よりGDアルゴリズムの有効性が確認されました。

図12 コンクリート供試体の振動応答の測定方法
参考論文 No.1
GDアルゴリズムが上記で仮定した数学モデルに一致することを確認するために、図1Aと図2Aに示す標準パターンと入力パターンの間の形状距離を算出する数値実験を行いました。
この数値実験から、GDアルゴリズムが数学モデルの条件<1>と<2>を満たすことが確認されました。
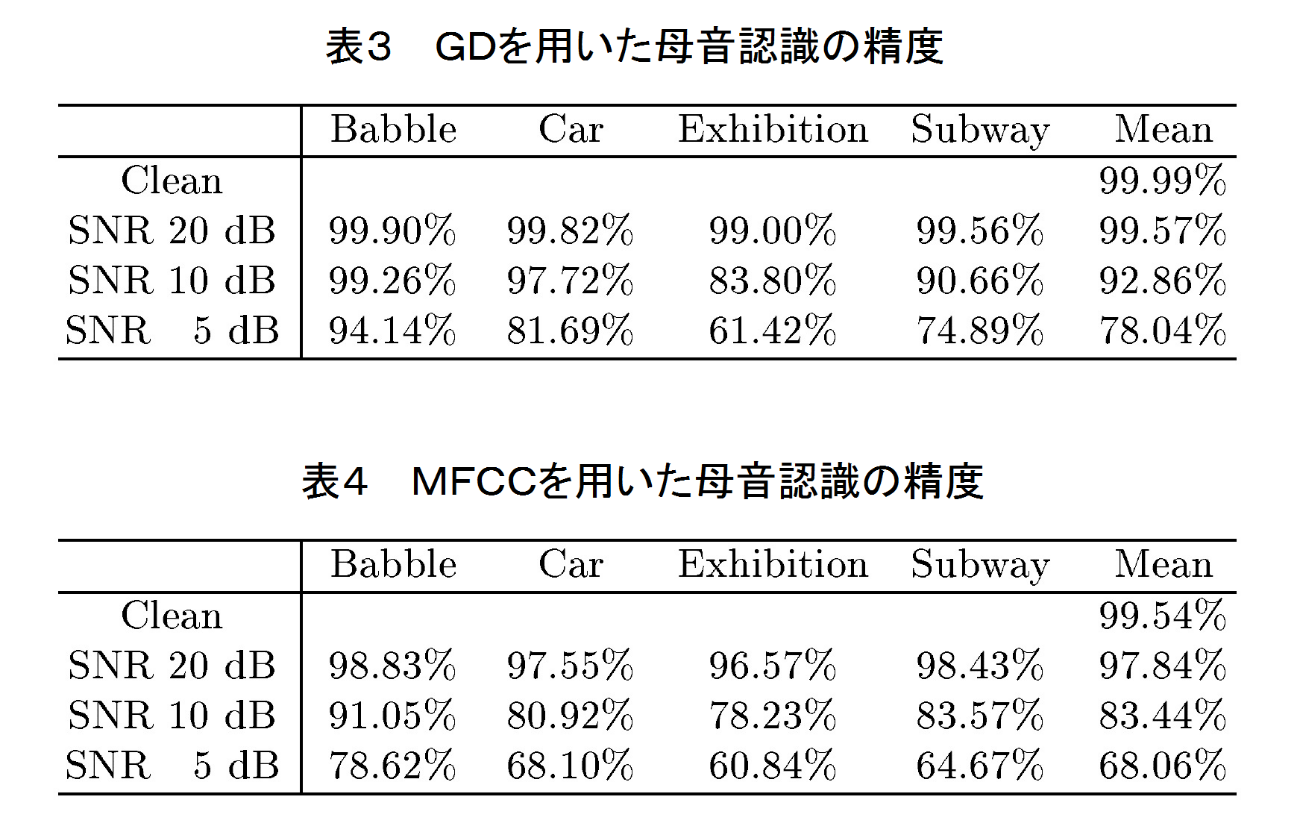
様々な種類の様々なSNRレベルの騒音環境下において母音認識実験を行いました。
表3と表4のそれぞれは、形状距離を用いた母音認識の結果とMFCC(Mel-Frequency Cepstrum Coefficients)を用いた母音認識の結果を示しています。
これらの表から、すべての場合において形状距離の認識精度がMFCCのそれよりも高いことが分かります。特に、10dBと5dBの平均では約10%の改善が見られます。このように数学モデルとGDアルゴリズムの有効性が確認されました。